Vermischte Übungen zu Bausteinen und zur Analyse von Algorithmen
Konfigurierbares Blinken
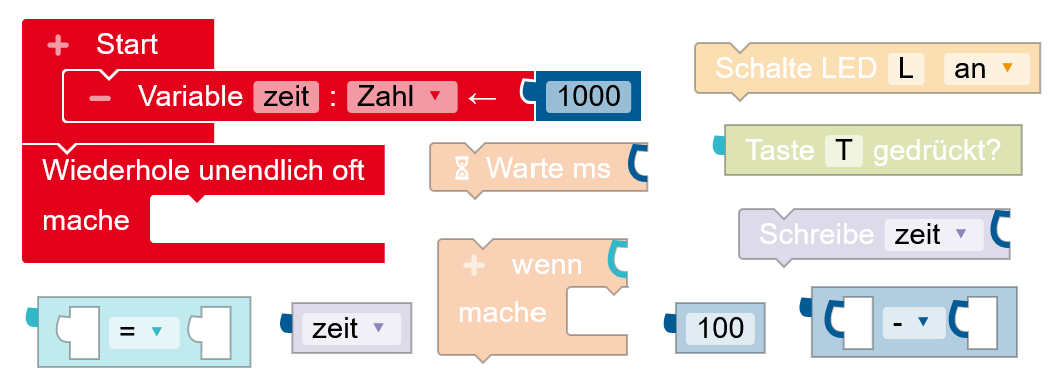
Am Arduino ist ein Taster und eine LED angeschlossen. Die LED soll zunächst jeweils eine Sekunde lang an sein und eine Sekunde aus. Mit dem Taster lässt sich die Zeit jedoch mit jedem Drücken um 100ms verringern. Wenn die Zeit dabei auf 200ms gestellt wird, wird sie stattdessen wieder auf 2000ms hochgesetzt.
- Zeichne einen Schaltplan und benenne die Größe der jeweils notwendigen Widerstände.
- Entwickle ein Programm nach den beschriebenen Anforderungen und stelle es als Struktogramm dar.
Hörbare Helligkeit
Am Arduino wird ein LDR und ein Piezo-Summer angebracht.
- Beschreibe mit einem Je-Desto-Satz das Verhalten des Widerstands des LDR, wenn es dunkel wird.
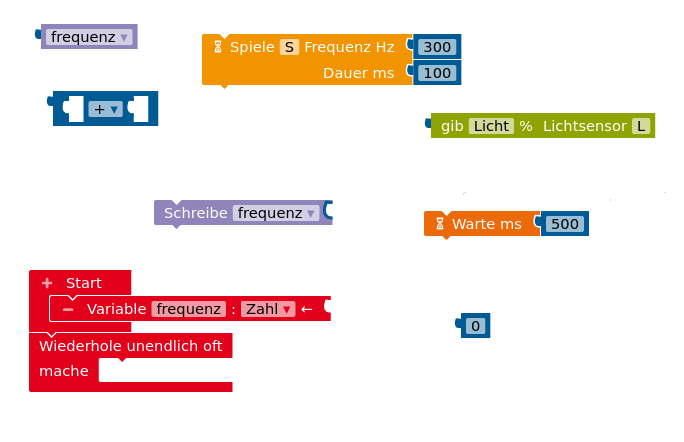
- Die Helligkeit wird mit einem Prozentwert zwischen 0 und 100 gemessen. Entwickle mit den unten abgebildeten Blöcken ein Programm, dass die Helligkeit in eine Tonhöhe zwischen 300Hz und 600Hz übersetzt und diesen Ton ausgibt. Stelle das Programm als Struktogramm dar.
Juke-Box 2.0

Logische Operationen lassen sich nutzen, um die Juke-Box vom Anfang des Kapitels zu erweitern, ohne Hardware nachrüsten zu müssen. Zur Erinnerung: Es wurden zwei Taster T1 und T2 und ein Piezo-Summer an den Arduino angeschlossen. Wenn Taster1 gedrückt wurde, gab der Befehl Taste T1 gedrückt? WAHR zurück und es wurde ein entsprechender Song gespielt.
Die Idee: Man kann auch beide Taster gleichzeitig oder gar keinen Taster drücken, sodass sich vier Fälle für vier Songs ergeben. Sinnvollerweise wird nur irgendeine Standardmusik gespielt, wenn gar kein Taster gedrückt wurde.
Formuliere für jeden der vier Fälle eine trennscharfe Bedingung!
Gesetze von de Morgan
Die Gesetze von de Morgan sagen aus, wie sich die Kombination des NICHT-Operators und des UND-Operators bzw. des ODER-Operators umformen lässt. Für zwei Aussagen A und B, die jeweils wahr oder falsch sein können, gilt:
(1) NICHT( A ODER B ) = NICHT( A ) UND NICHT( B ),
(2) NICHT( A UND B ) = NICHT( A ) ODER NICHT( B ).
Weise die Aussagen der Gesetze von de Morgan nach. Erstelle dazu für beide Seiten Wahrheitswerttabellen und zeige, dass für die gleiche Wahrheitswertkombination zu A und B immer auf beiden Seiten das gleiche Ergebnis herauskommt.
Zu (1):
links
A |
B |
A ODER B |
NICHT( A ODER B ) |
|---|---|---|---|
| 1 | 1 | 1 | ... |
| ... | ... | ... | ... |
rechts
A |
B |
NICHT( A ) |
NICHT( B ) |
NICHT( A ) UND NICHT( B ) |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | ... |
| ... | ... | ... | ... | ... |
Variablen und Datentypen
- Nenne Vorteile, die für die Verwendung von Variablen sprechen.
- Nenne drei Datentypen, die in Variablen gespeichert werden können.
Programme verstehen
Am Arduino wird an Pin 9 eine LED mit Vorwiderstand und an Pin 10 ein Piezo-Summer angebracht. Dann wird das folgende Programm ausgeführt.
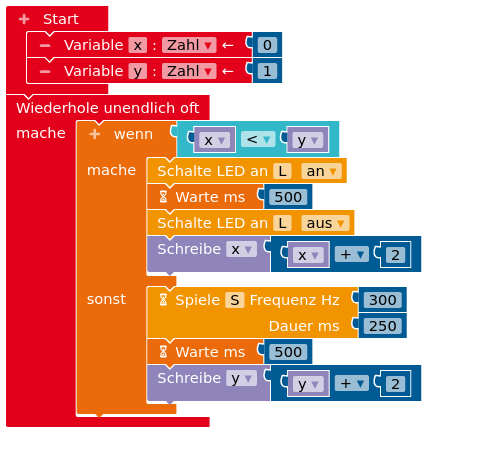
- Stelle das oben abgebildete Programm als Struktogramm dar.
- Beschreibe die Wirkung des oben abgebildeten Programms.
- Erkläre, wie man das Programm ändern müsste, damit die LED zwei Mal blinkt, bevor wieder der Piezo-Summer piept.
Zählschleife analysieren
An allen Digitalpins des Arduino wird eine LED mit Vorwiderstand angeschlossen. Dann wird das abgebildete Programm ausgeführt.
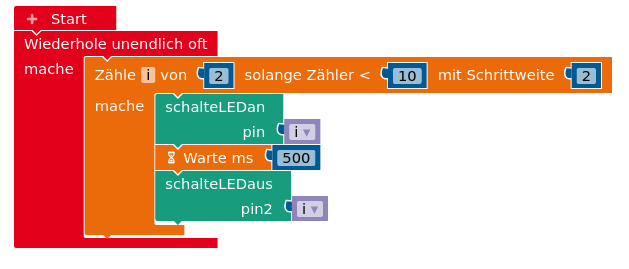
- Erstelle eine Trace-Tabelle für einen Durchlauf der
wiederhole unendlich oft-Schleife. - Nenne die Pin-Nummern der LEDs, die nach einem Durchlauf dieses Programms geleuchtet haben.
- Stelle das Programm als Struktogramm dar.
Zählschleifen für die Mathematik
Mit Hilfe der Zählschleifen im folgenden Programm sollen Eigenschaften von Zahlen untersucht werden.
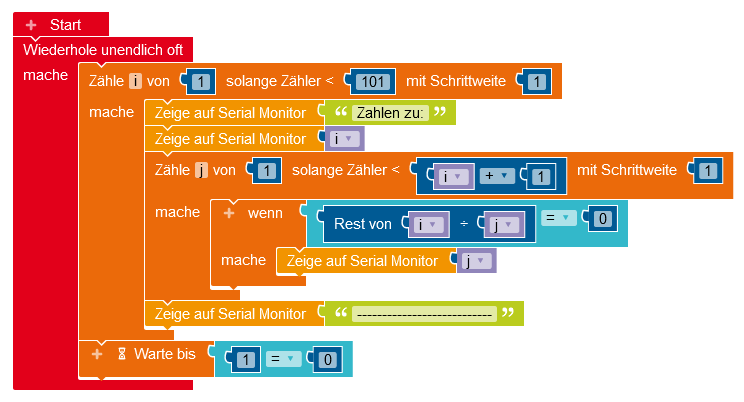
- Bestimme für
i=1bisi=5welche Zahlen auf dem seriellen Monitor ausgegeben werden. - Erkläre allgemein, welche Zahlen auf dem seriellen Monitor ausgegeben werden.
EVA am Smartphone
- Nenne jeweils drei Bauteile im Smartphone, die für die Eingabe bzw. für die Ausgabe zuständig sind.
- Anne schreibt Bernd mit ihrem Smartphone eine Textnachricht. Bernd empfängt diese auf seinem Smartphone. Kategorisiere den Prozess auf Annes und auf Bernds Smartphone jeweils nach dem EVA-Prinzip.